What are the odds and why?
My my first inclination was that answer 1 was correct when I was given this problem. And here is why: If you take away one of the choices, you are left with only two doors. And anyone can tell you that choosing between two things is a 50-50 proposition, just like a coin toss. But there is a snag with this reasoning. You are not choosing between two equal things!
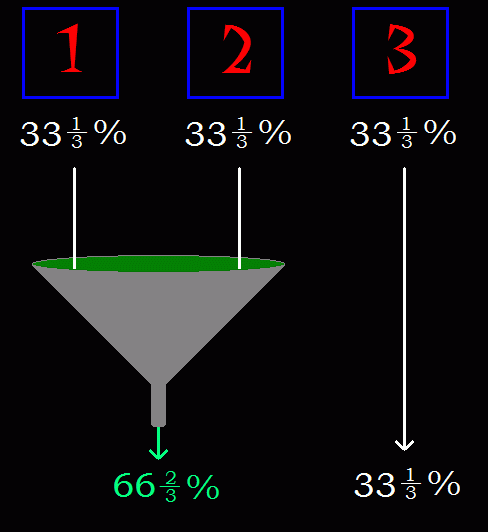
When you reach the point where Monte is going to expose a door, but has not yet done so, you know that you have a 33% chance of having the car, because 1 door has the car and two of the doors do not.
Monte knows which door has the car, and so if the car is behind either 1 or 2, he will select the other one and expose it. That means he is filtering two chances that the car is there into a single choice for you.
Notice that he has given you no new information concerning your door (you already knew that one of those other two doors did not have the car), and so the odds remain at 33% that you have the right door, but he has given you new information about the remaining door, and he has doubled the odds that the remaining door has the car behind it!
Remember that if the car is behind door #1, then Monte will expose door #2. If the car is behind door #2 then he will expose door #1. The remaining door that you did not select suddenly becomes twice as likely to be the one where the car is located because if the car is behind either door #1 or door #2 it will now be behind the door that you have not picked. Instead of a 50-50 proposition between two equal choices, you are left with a choice between your first pick with odds of 33.33% of being correct, and switching to the remaining door with odds of 66.67% of being correct. Your best bet is to switch, and answer #2 is corrrect.
|